满射(或称全射)是数学中集合论和函数论中的一个概念,它描述了一种特殊的映射关系,在满射中,一个集合中的每个元素都被映射到另一个集合中的唯一元素,下面将详细解释满射的概念,并使用小标题和单元表格进行说明。
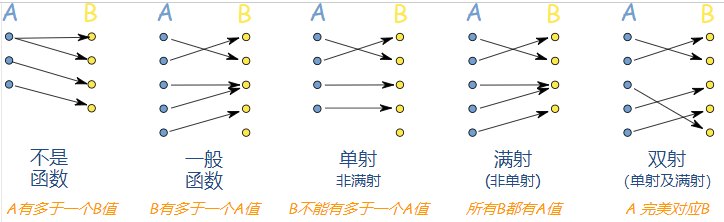
(图片来源网络,侵删)
1. 定义
满射是指从一个集合A到另一个集合B的映射f,满足对于任意的a属于A,都有唯一的b属于B,使得f(a) = b,换句话说,满射确保了从A到B的映射是“一一对应”的。
2. 符号表示
满射通常用箭头符号表示,
[ f: A rightarrow B ]
其中A和B分别是输入和输出的集合。
3. 示例
考虑以下两个集合A和B:
[ A = {1, 2, 3} ]
[ B = {4, 5, 6} ]
我们可以定义一个满射f如下:
[ f(1) = 4 ]
[ f(2) = 5 ]
[ f(3) = 6 ]
在这个例子中,集合A中的每个元素都被映射到集合B中的唯一元素,因此f是一个满射。
4. 与单射的关系
满射和单射(或称为一一对应)之间存在密切的关系,如果一个映射既是单射又是满射,那么它被称为双射,双射是一种特殊的映射,它将一个集合的元素与另一个集合的元素完全对应起来。
5. 性质和应用
满射具有以下性质:
如果f是从A到B的满射,那么对于任意的b属于B,都存在唯一的a属于A,使得f(a) = b,这称为逆映射的存在性。
如果f是从A到B的满射,那么f的图像(即所有被映射到的元素的集合)等于集合B,这称为映射的核的性质。
如果f是从A到B的满射,并且g是从B到C的满射,那么复合映射f∘g也是从A到C的满射,这称为复合映射的性质。